The Joy of Garden Math
Your content goes here. Edit or remove this text inline or in the module Content settings. You can also style every aspect of this content in the module Design settings and even apply custom CSS to this text in the module Advanced settings.
Despite what you thought in high school, math can be useful
Maybe you think you don’t need math to get by in this world. And maybe you’re right. But then again, maybe math can make your life just a little easier.
This month, I’ll discuss some useful math concepts that we can use for gardening. If you’re one of the many who hated math in school and only dealt with it so you could graduate, maybe you’ll see how there might be some use for it after all.
Has this ever happened to you?
The bag says 3.8 lb of fertilizer will cover 1000 sq ft, and your lot is a quarter acre. The book says your tree needs six inches of water, and your drip emitters provide one gallon per hour. Mulch is $6 per cubic yard, and your garden is 25 feet by 12 feet. How do we figure it out? Now do you wish you’d paid attention in math class? Well, if you finish this article, maybe you’ll earn your nerd badge after all.
Distance First, let’s talk about measuring distance. Why is it important? So you can know how much fencing you need or how much drip tubing you need to reach the end of a row. Just get out your trusty tape measure and you’re ready, right? Indeed you are.
I’m sure you have this concept well in hand. We usually measure in feet and inches, and you certainly know that 3 feet make a yard. We won’t get into centimeters and stuff because, darn it, this is America.
You can measure up and down, across, and front to back, and around something. In other words, we can measure length, width, height, and girth.
Also remember that we can convert inches to feet and yards to inches or whatever we need. There are 12 inches in a foot, so if you measure 74 inches, just divide by 12 and you get 6 feet plus the remainder of 2 inches.
Say you measure 5 feet 6 inches where you need to insert a run of drip tubing. The store has rolls of tubing with a label saying it is 72 inches long. Is one roll enough? Your measurement is 5 feet 6 inches. Whip out your handy-dandy calculator (maybe on your cell phone), and figure 5 x 12 + 6 or 66 inches. Great – you only need one roll of tubing.
What if you need enough tubing to circle a tree? A long time ago someone noticed that the distance around the edge of a circle (the circumference) was always 3.14 times the width (or diameter) of the circle, no matter how big or how small.
The constant 3.14 is called pi (say “pie”), which is the greek letter π. So if you want a circle of drip tubing around your tree at a distance of 6 feet, let’s think about it. The tree is the center of a circle, and the tubing is 6 feet out from the center. That means the circle is 12 feet across, right? That’s the diameter (or d). So the length of the tubing is the circumference of the 12 foot circle, which is π x d or 3.14 times 12 feet = about 38 feet. Most calculators have a key for pi these days, although you might have to switch to “scientific view”. It might be labeled either “pi” or ”π”.
Area OK, measuring distance in feet and inches isn’t all that hard. Let’s move on to measuring area, which is the size of a flat shape. Why is it important? Well, the fertilizer bag said 3.8 lb will cover 1000 square feet, so measure your garden or lawn to see how many pounds of fertilizer to use.
You calculate the area of a square or rectangle by multiplying length x width. Area is usually expressed as square units, such as square inches
or square feet. But “acre” is commonly used; you can look up how many square feet are in an acre.
You might picture a room covered with tiles that are each 1 foot square; count them and you have the area in square feet. But you’ll get the same answer if you measure the length and width of the room and multiply.
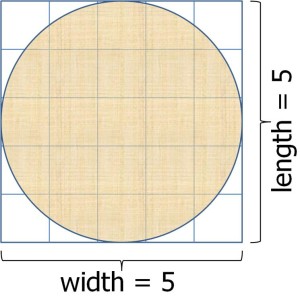
But what if your garden is round? The figure below shows a round garden (a circle) drawn within a square garden.
The round garden is just as long and just as wide, but you can see that it must have less area because the corners are cut off. Now what? Pi to the rescue again. Math books tell us the area of a circle is π r2 . In this formula, “r” stands for the radius of the circle. When you draw a circle with a compass, the point is at the center and the pencil tip is at the edge. That distance is the radius.
Obviously the radius is 1/2 the diameter. And we don’t need an “x” for “times”. It’s implied. Also, in math any number times itself is called “square”, and we write it with that little 2 up high. For this circle, the area is 3.14 x 2.5 x 2.5 = 19.6 sq in. The area of the square is 5 x 5 = 25 sq in, so the circle has a smaller area as we surmised from the figure.
As an example, maybe you want to put compost in the 12 foot wide circle around that tree with the tubing. Then π r2 is 3.14 times 6 squared, which is 3.14 x 36 = just over 113 square feet of area to cover.
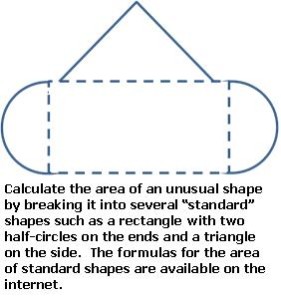
What if your turf is a kidney shape, or your garden is an oval? You can google the formula of any “standard” shape like a circle or triangle. Unusual shapes will require that you sketch them as several standard shapes crunched together, like a half-circle on each end of a rectangle with a triangle on the side.
Once you know the area of your turf or garden, you can figure out how much water or fertilizer to apply.
Volume The last concept we’ll discuss is volume. Where distance is how wide or long or tall or far around something is, and area is how big a flat thing is, volume is how much something will hold. To figure that, we’re going to multiply length times width times height, which is area x height.
Distance is in inches or feet, area is in square inches or square feet, and volume is in “cubic” inches or “cubic” feet. You got it – feet x feet x feet comes out feet3 or “cu ft”. Same with inches or yards.
Besides cubic feet, cubic inches, etc., we commonly state volume measurements as gallons, quarts, cups, liquid ounces, and so forth. And yes, we can convert between all these volume measurements.
Why is it important? Volume will tell you how much water or mulch or compost you need to cover an area to a certain depth.
Say you want to cover 450 sq ft of landscape with 3 inches of gravel, which is sold by the cubic yard (they just say “yard”). But maybe the minimum order of gravel for delivery is three (cubic) yards, and if you need 4 yards but order 3, how will you get the other yard of gravel after you see that you’re short? You can’t order 1 more yard for delivery. And if you order 5 or 6 yards and use 4, you’re going to need to get that extra gravel out of your driveway, and a yard of gravel can weigh a ton and a half.
So a gardener really can make handy use of math. Of course, you can ask the gravel yard how much you need to cover 450 sq ft at 3 inches, and maybe that’s a good idea even if you do the calculations yourself, because who wants to come up short?
Volume is area times height, so we multiply our 450 sq ft of area by 3 inches of gravel. Shoot. Can you multiply feet by inches? Better not. Instead, figure 3 inches is 3/12 of a foot. I know, fractions can be scary. But you know how many inches are in a foot, and how many feet are in a yard, so you can do this! You just converted 3 inches to 3/12 foot, which your calculator will tell you is 0.25 feet. See? Your calculator can help with this. Try it. 3 divided by 12 is 0.25. So the volume of gravel we need is 450 sq ft x 0.25 ft = 112.5 cubic ft.
Easy enough. But how many cubic yards is 112.5 cu ft?
A cubic yard is 1 yard x 1 yard x 1 yard. How many feet in a yard? Three. So figure it again: 3 feet x 3 feet x 3 feet = 27 cu ft to 1 cu yd. We’re getting closer now. We need 112.5 cu ft and there are 27 cu ft in a cu yd. That’s like, “How many $20 shirts can you buy if you have $100?” You divide, right? So 112.5 cu ft divided by 27 cu ft per cu yd gives you 4.16 cu yd. Since you can’t order .16 yard, decide if you order 4 yards of gravel and spread it a little thin or 5 yards and spread it thicker.
Note: Sometimes gravel is sold by the ton. Just ask them how many yards are in a ton. It might vary a little for different kinds of gravel.
As another example of volume, let’s consider soil moisture content. In class we learned about “inches of water” in soil, and your book says your tree needs 36 inches of water annually. But your dripper emits 1 gallon of water per hour (1 gph). How do we relate inches to gallons?
We’ll discuss irrigation another time, but for now let’s just consider a 1 foot circle on the ground around where a single emitter lies (how wide the circle actually is depends on the soil type and the drip rate, but let’s assume 1 foot for now). The area of the circle is π r2, or 3.14 times 6 inches squared, which is 3.14 x 36 = just over 113 square inches.
Our SCMG manual tells us that sandy loam soil has a “field capacity” or moisture holding capacity of about 2 inches of water per foot. Since the root zone for a tree goes down about 3 feet, the most water we can apply without waste is about 2 in/ft x 3 ft = 6 inches. Multiply the area of our circle by 6 inches of water depth and we get 113 sq in x 6 in = 678 cu in of water.
Now the magic: google “cubic inches per gallon” and you will discover that a gallon of water is 231 cu in. How many gallons are in 678 cu in? Divide 678 by 231 and you get 2.9 gallons.
We would have to run the drip system for 2.9 hours since we get 1 gallon per hour. Any more than that and the water is wasted because it goes beyond the root zone.
Final Exam
Congratulations if you have read this far! You obviously have a bit of geek in you.
To earn the coveted nerd badge in math, solve the following problem:
To get the most for your money, should you buy two 10 inch pizzas at $5 each, or one 20 inch pizza for $15?
Show your work. And you better answer one 20 inch pizza.
About fractions, “units”, and conversion factors:
The slash in a fraction means “divided by”. 1/3 means a whole divided by three. Maybe when you were learning fractions you pictured a pie cut into 3 parts, each one being 1/3 of a pie. Put them all together and you get 1/3 + 1/3 + 1/3 = 3/3, meaning you have a whole pie again. If you have the same denominators, you can add the numerators. But if you’re multiplying fractions, you multiply the numerators and you multiply the denominators, like this: 2/3 x 1/2 = 2/6, which is the same as 1/3 if you divide both top and bottom by 2. It makes sense because 1/2 of 2/3 should be 1/3, shouldn’t it?
If a fraction has the same numerator and denominator, it is equal to one. Consider 3/3. You read it as “3 thirds”, and of course 3 thirds is a whole, which is one. Any value multiplied by one is unchanged: for example, 5 x 1 = 5. So if we multiply any number by 1 yd3/27 ft3, the value isn’t changed because 1 yd3 is equal to 27 ft3 and therefore 1 yd3/27 ft3 has a value of one. But “units” like ft3 in the numerator and denominator can “cancel” . For example, 5 ft x 12 in/1 ft = 60 in. The “feet” in the numerator and the denominator cancel, and the answer is left in inches.
We read a conversion factor, such as 12 in/1 ft, as “twelve inches per 1 foot”. 1 yd3/27 ft3 is “one cubic yard per 27 cubic feet”. So “12 in/1 ft” is a conversion factor, which can also be used as “1 ft/12 in” to convert units from inches to feet. The same goes for 1 yd3/27 ft3 and 1 gallon/231 cu in. Multiplying by a conversion factor is multiplying by one, but it converts units to get the answer we need.